엔트로피

정보량이란 '놀라움의 정도'를 의미한다. 즉 얼마나 새로운 정보를 얻을 수 있는지를 이야기한다.

정보량은 확률이 낮을수록 크다. 

확률은 새롭지 않은 정보를 나타낸다. 예를 들어 비올 확률이 80%일 때 비가 오면 우린 이미 확률 80%로 비올 정보를 알고 있었던 것이다. 그렇지만 비가올 확률이 80%인데 비가 오지 않는다면 이는 확률로 표현되지 않은 새로운 정보를 얻은 것이다.

이것이 바로 정보량인 것이다!

수식으로는 다음과 같이 표현한다.

정보량

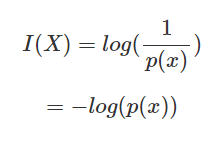
엔트로피(Entropy)란 확률 분포의 정보량이다. 다시 말하면 정보량에 대한 평균, 또한 기댓값에 대한 불확실성이라고 생각하면 된다.

수식으로 표현하면 다음과 같다.

엔트로피

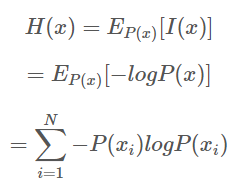
그렇다면 Joint entropy는 무엇일까?

Joint Entropy는 두 확률 변수의 결합 엔트로피이다. 즉 교집합의 엔트로피라고 생각하면 된다.

Joint Entropy

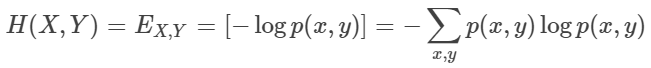
Joint Entropy와 가장 많이 헷갈리는 것 중하나는 바로 Cross Entropy이다.

Cross Entropy는 두 확률 분포 p, q가 있을 때 p 대신에 q를 사용하여 p를 설명할 때 필요한 정보량이라고 이해한다.

Cross Entropy

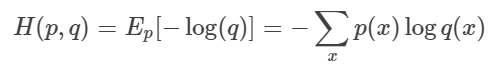
Conditional Entropy는 어떠한 사건이 일어났을 때 다른 사건의 불확실성을 나타낸다.

아래 수식에서는 X 사건이 일어났을 때 Y의 불확실성을 나타낸다.

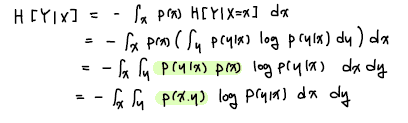
연두색 부분은 확률론에서 가장 많이 쓰이는 베이지안 추론이다.

베이지안 추론이야말로 GAN이나 VAE와 같은 생성 모델을 다루게 되면 가장 많이 보게 되는 부분이다.

아래 수식에서는 추론 대상 H에 대해서 사전 확률 p(H)가 주어진다.

H와 관계된 관측 E의 확률 분포가 p(E|H)로 주어지다고 할 때, 베이즈 추론은 E가 추가적으로 주어졌을 때 H의 분포 p(H|E)를 계산한다.

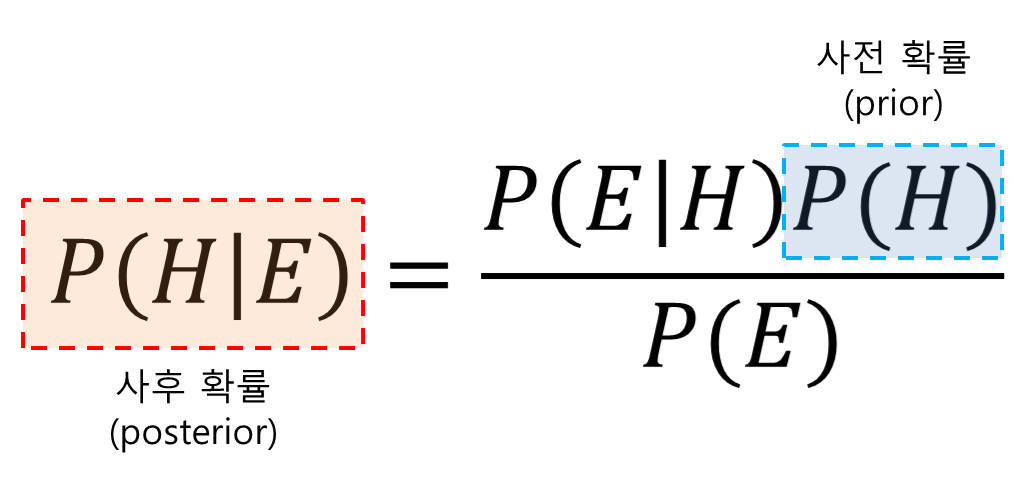
상호 정보량(Mutual Information)은 무엇일까?

상호 정보량은 Y가 어떠한 값으로 정해졌을 때 X의 불확실성을 의미한다.

만약 X, Y가 독립적이라면 서로 아무런 영향을 못주기 때문에 Y값이 정해진다고 한들 영향이 없다.

즉 X는 여전히 불확정적이라는 의미이다.

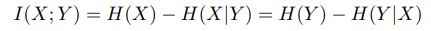
상호 정보량을 두 확률 변수 X,Y에 대해 Joint Distribution과 True Distribution간의 쿨백라이블러 발산으로 표현할 수 있다.

 

여기서 쿨백 라이블러 발산(KL-divergence)는 두 확률 분포의 차이를 계산하는 함수이다. 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링한다면 발생할 수 있는 정보 엔트로피 차이를 구하는데 보통 많이 사용된다.

KL-divergence

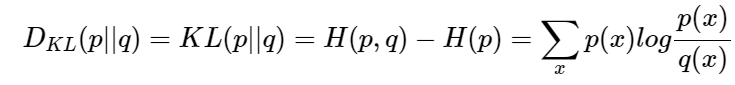
쿨백 라이블러 발산의 특징은

• 항상 0보다 크다.
• 비대칭적이다. --> KL(p,q)와 KL(q,p)는 같을 수 없다.
• 두 확률 분포가 동일할 때 KL-Divergence는 0이 된다.

위에서 Cross Entropy를 통해 KL-Divergence를 유도할 수 있다.

상호 정보량이 딥러닝에 쓰이게 되면 아래와 같이 된다.

---

참고자료

https://datascienceschool.net/02%20mathematics/10.04%20%EC%83%81%ED%98%B8%EC%A0%95%EB%B3%B4%EB%9F%89.html