| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 융합연구
- Vae
- panoptic segmentation
- Deep Learning
- NERF
- 리눅스
- 파이토치
- Computer Vision
- CVPR2023
- Neural Radiance Field
- GAN
- panoptic nerf
- 논문 리뷰
- 2022
- 경희대
- pytorch
- 논문리뷰
- 딥러닝
- CVPR
- paper review
- linux
- ICCV 2021
- ICCV
- Semantic Segmentation
- Python
- 논문
- IROS
- docker
- Paper
- NeRF paper
- Today
- Total
윤제로의 제로베이스
로지스틱 회귀 (Logistic Regression) 본문
01. 로지스틱 회귀(Logistic Regression)
일상 속 풀고자하는 많은 문제 중에서는 두 개의 선택지 중에서 정답을 고르는 문제가 많습니다. 예를 들어 시험을 봤는데 이 시험 점수가 합격인지 불합격인지가 궁금할 수도 있 ...
wikidocs.net
1. 이진 분류 (Binary Classification)
- 둘 중 하나를 결정하는 문제를 이진 분류(Binary Classification)이라고 한다.
2. 시그모이드 함수(Sigmoid function)
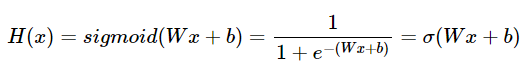
%matplotlib inline
import numpy as np # 넘파이 사용
import matplotlib.pyplot as plt # 맷플롯립사용
def sigmoid(x): # 시그모이드 함수 정의
return 1/(1+np.exp(-x))1) W가 1이고 b가 0인 그래프
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y, 'g')
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()
위으 그래프에서 시그모이드 함수는 출력값을 0과 1사이의 값으로 조정하여 반환한다.
x가 0일 때의 값을 가진다. x가 매우 커지면 1에 수렴한다. 반면 x가 작아지면 0에 수렴한다.
2) W값의 변화에 따른 경사도의 변화
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(0.5*x)
y2 = sigmoid(x)
y3 = sigmoid(2*x)
plt.plot(x, y1, 'r', linestyle='--') # W의 값이 0.5일때
plt.plot(x, y2, 'g') # W의 값이 1일때
plt.plot(x, y3, 'b', linestyle='--') # W의 값이 2일때
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()
가중치 W값이 커지면 경사가 커지고 W값이 작아지면 경사가 작아진다.
3) b값의 변화에 따른 좌, 우 이동
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(x+0.5)
y2 = sigmoid(x+1)
y3 = sigmoid(x+1.5)
plt.plot(x, y1, 'r', linestyle='--') # x + 0.5
plt.plot(x, y2, 'g') # x + 1
plt.plot(x, y3, 'b', linestyle='--') # x + 1.5
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()
4) 시그모이드 함수를 이용한 분류
시그모이드 함수는 입력값이 한없이 커지면 1에 수렴하고, 입력값이 한없이 작아지면 0에 수렴한다.
시그모이드 함수의 출력값은 0과 1 사이의 값을 가지는데, 이 특성을 이용하여 분류 작업을 할 수 있다.
3. 비용 함수(Cost function)
앞서 선형 회귀에서 배운 비용 함수인 평균 제곱 오차(Mean Square Error, MSE)를 로지스틱 회귀의 배용 함수로 사용하면 어떨까.

위의 그래프에서 경사 하강법을 사용하게 되면 경사 하강법이 오차가 최소값이 되는 구간에 도착했따고 판단하는 구간이 실제 오차가 최소값이 되는 구간이 아닐 수도 있다는 점이다.
이를 전체 함수에 걸쳐 최소값인 글로벌 미니멀(Global Minimum)이 아닌 특정 구역에서의 최소값인 로컬 미니멈(Local Minimum)에 도달했다고 한다.
시그모이드 함수의 특징은 함수의 출력값이 0과 1 사이의 값이라는 점이다. 즉, 실제 값이 1일 때 예측값이 0에 가까워지면 오차가 커져야 하며, 실제값이 0일떄, 예측값이 1에 가까워지면 오차가 커져야한다.
이를 충족하는 함수가 로그 함수이다.
실제값이 1이라면 예측값인 H(x)의 값이 1이면 오차가 0이므로 cost는 0이 된다. 반면 H(x)가 0에 수렴하면 cost는 무한대로 발산한다. 즉 로그 함수를 식으로 표현하면 다음고 같다.



정리하자면, 위 비용 함수는 실제값 y와 예측값 H(x)의 차이가 커지면 cost가 커지고, 실제값 y와 예측값 H(x)의 차이가 작아지면 cost는 작아진다. 이 비용 함수에 대해 경사 하강법을 수행하면서 최적의 가중치 W를 찾아간다.
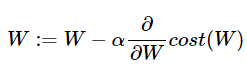
4. 파이토치로 로지스틱 회귀 구현하기
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data) # 크기는 6 x 2
y_train = torch.FloatTensor(y_data) # 크기는 6 x 1
W = torch.zeros((2, 1), requires_grad=True) # 크기는 2 x 1
b = torch.zeros(1, requires_grad=True)
# torch.exp()를 이용하여 시그모이드
hypothesis = 1 / (1 + torch.exp(-(x_train.matmul(W) + b)))
# torch.sigmoid()를 이용하여 시그모이드
hypothesis = torch.sigmoid(x_train.matmul(W) + b)
# 비용 함수 직접 구현
losses = -(y_train * torch.log(hypothesis) + (1 - y_train) * torch.log(1 - hypothesis))
cost = losses.mean()
# F.binary_cross_entropy(예측값, 실제값)dmf tkdyd
F.binary_cross_entropy(hypothesis, y_train)'Background > Pytorch 기초' 카테고리의 다른 글
| 클래스로 로지스틱 회귀 모델 구현하기 (0) | 2022.01.16 |
|---|---|
| nn.Module로 구현하는 로지스틱 회귀 (0) | 2022.01.16 |
| 커스텀 데이터셋 (Custom Dataset) (0) | 2022.01.16 |
| 미니 배치와 데이터 로드 (Mini Batch and Data Load) (0) | 2022.01.16 |
| 클래스로 파이토치 선형회귀 모델 구현하기 (0) | 2022.01.14 |
