| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- Vae
- Neural Radiance Field
- CVPR
- 융합연구
- NERF
- 논문 리뷰
- Computer Vision
- linux
- 경희대
- panoptic nerf
- 딥러닝
- CVPR2023
- Deep Learning
- 논문리뷰
- pytorch
- paper review
- docker
- NeRF paper
- IROS
- ICCV 2021
- Semantic Segmentation
- 파이토치
- GAN
- Python
- 리눅스
- panoptic segmentation
- ICCV
- 2022
- Paper
- 논문
- Today
- Total
윤제로의 제로베이스
글로브(GloVe) 본문
06. 글로브(GloVe)
글로브(Global Vectors for Word Representation, GloVe)는 카운트 기반과 예측 기반을 모두 사용하는 방법론으로 2014년에 미국 스탠포드대 ...
wikidocs.net
글로브(Global Vectors for Word Representations, GloVe)는 카운트 기반과 예측 기반을 모두 사용하는 방법론으로 2014년 미국 스탠포드대학에서 개발한 단어 임베딩 방법론이다.
기존의 카운트 기반의 LSA(Latent Semantic Analysis)와 예측 기반의 Word2Vec의 단점을 지적하며 이를 보완한다느 목적으로 나왔으며, 실제로도 Word2Vec만큼 뛰어난 성능을 보인다.
1. 기존 방법론에 대한 비판
LSA는 단어의 빈도수를 카운트 한 행렬이라는 전체적인 통계 정보를 입력으로 받아 차원을 축소(Truncted SVD)하여 잠재된 의미를 이끌어내는 방법론이다.
반면, Word2Vec는 실제값과 예측값에 대한 오차를 손실 함수를 통해 줄여나가며 학습하는 예측 기반의 방법론이다.
LSA는 왕:남자=여왕:? 과 같은 단어 의미 유추 작업(Analogy task)에서는 성능이 떨어진다.
Word2Vec는 예측 기반으로 단어간 유추 작업은 뛰어나지만, 임베딩 벡터가 윈도우 크기 내에서만 주변 단어를 고려하기 때문에 코퍼스의 전체적인 통계정보를 반영하지 못한다.
GloVe는 이러한 기존 방법론들의 각각의 한계를 지적하며, 두가지 방법론을 모두 사용한다.
2. 윈도우 기반 동시 등장 행렬(Window based Co-occurence Matrix)
단어의 동시 등장 행렬은 행과 열을 전체 단어 집합의 단어들로 구성하고, i 단어의 윈도우 크기 내에서 k단어가 등장한 횟수를 i행 k열에 기재한 행렬을 말한다.
위 행렬은 전치해도 동일한 행렬이 된다는 특징이 있다.
그 이유는 i단어의 윈도우 크기 내에서 k단어가 등장한 빈도는 반대로 k 단어의 윈도우 크기 내에서 i 단어가 등장한 빈도와 동일하기 때문이다.
3. 동시 등장 확률(Co-occurrence Probability)
동시 등장 확률은 동시 등장 행렬로부터 특정 단어 i의 전체 등장 횟수를 카운트 하고, 특정 단어 i가 등장했을 때 어떤 단어 k가 등장한 회수를 카운트하여 계산한 조건부 확률이다.
4. 손실 함수(Loss function)

GloVe는 임베딩 된 중심 단어와 주변 단어 벡터의 내적이 저체 코퍼스에서의 동시 등장 확률이 되도록 만드는 것이다.
즉, 이를 만족하도록 임베딩 벡터를 만드는 것이 목표이다.
이를 식으로 표현하면 다음과 같다.
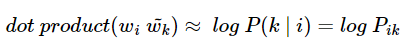

아직 함수 F가 어떤 식을 가지고 있는진 알 수 없다.
위의 목적에 맞게 근사할 수 있는 함수식은 무수히 많겠지만 최적의 식을 만들기 위해 디테일을 추가한다.
함수 F는 두 단어 사이의 동시 등장 확률의 크기 관계 비 정보를 벡터 공간에 인코딩 하는 것이 목표이다.
이를 위해서 연구진은 아래와 같은 F를 제안한다.

우변은 스칼라값이과 좌변은 벡터값이기 때문에 이를 성립하게 하기 위해서 F의 두 입력에 내적을 수행한다.
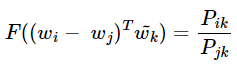
정리하면 선형 공간에서 단어의 의미 관계를 표현하기 위해 뺄셈과 내적을 택한 것이다.
여기서 함수 F가 만족해야하는 필수 조건이 있다.
중심 단어와 주변 단어라는 선택 기준은 실제로 무작위 선택이므로 이 둘의 관계는 자유롭게 교환이 가능해야한다.
이것이 성립되기 위해서 함수 F가 실수의 덧셈과 양수의 곱셈에 대해서 준동형(Homomorphism)을 만족하도록 한다.
정라하자면 a와 b에 대해서 F가 F(a+b) = F(a)F(b)가 되도록 만족시켜야 한다는 의미이다.
준동형식에서 a와 b가 각각 벡터값이라면 함수 F의 결과값으로는 스칼라 값이 나올 수 없지만, a와 b가 각각 벡터의 내적값이라고 하면 결과 값으로 스칼라 값이 나올 수 있다.
그러므로 위의 준동형 식을 아래와 같이 바꿀 수 있다.

그런데 앞서 작성한 GloVe 식에서는 w_i와 w_j라는 두 벡터의 차이를 F의 입력으로 받았다.
GloVe 식에 바로 적용을 위해 준동형식을 뺄셈에 대한 준동형식으로 변경한다.
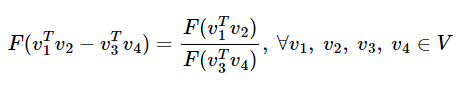
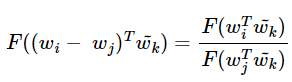
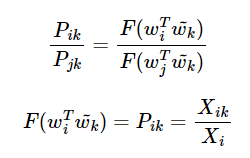

이는 뺄셈에 대한 준동형 식과 형태가 일치한다.
이제 이를 만족하는 F를 찾아야 한다.
F를 지수함수 exp라고 하자.
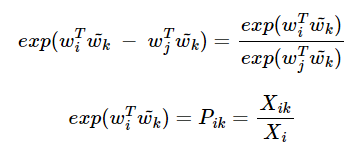

여기서 상기해야할 것은 앞서 언급했듯 중심단어와 주변 단어의 값은 위치를 서로 바꾸어도 성립해야 한다.
X_ik의 정의를 생각해보면 X_ki와 같다.
하지만 이것이 성립되려면 위의 식에서 logX_i가 걸림돌이다.
그래서 GloVe는 logX_i항을 편향이라는 상수로 대체하기로 한다.

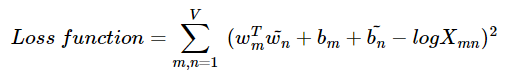
여기서 V는 단어 집합의 크기를 의미한다.
그런데 아직 최적의 손실함수라고 하기에는 부족한 점이 있다.
logX_ik에서 X_ik값이 0이 될 수 있다는 것이다.
이에 대한 대안으로 LogX_ik를 log(1+X_ik)항으로 바꾸게 된다.
하지만 여전히 문제가 존재하는데 바로 동시 등장 행렬 X는 마치 DTM처럼 희소 행렬일 가능성이 있다는 점이다.
동시 등장 행렬 X에는 많은 값이 0이거나, 동시 등장 빈도가 적어서 많은 값이 작은 수치를 가지는 경우가 많다.
앞서 빈도수를 가지고 가중치를 주는 고민을 하는 TF_IDF나 LSA와 같은 방법들을 본 적이 있다.
GloVe는 동시 등장 빈도 값 X_ik값이 굉장히 낮은 경우 정보에 거의 도움이 되지 않는다고 판단한다.
그래서 X_ik값에 영향을 받는 가중치 함수를 손실 함수에 도입하게 된다.
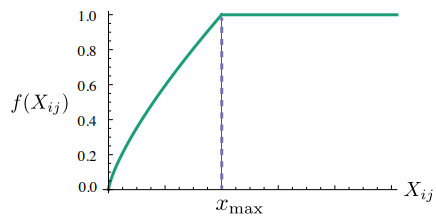
X_ik의 값이 작으면 상대적으로 함수의 값은 작도록 하고, 값이 크면 함수의 값은 상대적으로 크도록 한다.
하지만 X_ik값이 지나치게 높다고 해서 지나친 가중치를 주지 않기 위해서 함수의 최대값이 정해져 있다.
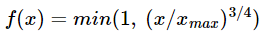

'Background > Pytorch 기초' 카테고리의 다른 글
| 순환 신경망(Recurrent Neural Network, RNN) (0) | 2022.01.26 |
|---|---|
| 파이토치의 nn.Embedding() (0) | 2022.01.26 |
| 워드투벡터(Word2Vec) (1) | 2022.01.26 |
| 워드 임베딩(Word Embedding) (0) | 2022.01.19 |
| NLP에서의 원-핫 인코딩(One-hot encoding) (0) | 2022.01.19 |



