| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- ICCV
- pytorch
- 논문 리뷰
- panoptic nerf
- Computer Vision
- Vae
- docker
- ICCV 2021
- NeRF paper
- 리눅스
- Paper
- 경희대
- GAN
- IROS
- Python
- linux
- 딥러닝
- 논문
- NERF
- CVPR
- 논문리뷰
- Deep Learning
- 2022
- paper review
- Semantic Segmentation
- CVPR2023
- 융합연구
- Neural Radiance Field
- panoptic segmentation
- 파이토치
- Today
- Total
윤제로의 제로베이스
역전파(Backpropagation) 본문
04. 역전파(BackPropagation)
인공 신경망이 순전파 과정을 진행하여 예측값과 실제값의 오차를 계산하였을 때 어떻게 역전파 과정에서 경사 하강법을 사용하여 가중치를 업데이트하는지 직접 계산을 통해 이해해봅 ...
wikidocs.net
1. 인공 신경망의 이해(Neural Network Overview)
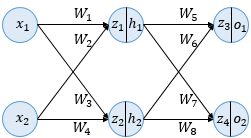
2. 순전파(Forward Propagation)

각 입력은 입력층에서 은닉층 방향으로 향하면서 각 입력에 해당하는 가중치와 곱해지고, 결과적으로 가중합으로 계산되어 은닉층 뉴런의 시그모이드 함수에 입력되게 된다.
z_1과 z_2는 시그모이드 입력으로 사용되는 값에 해당한다.
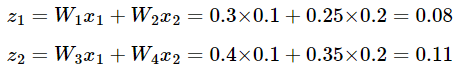
z_1과 z_2는 은닉층의 뉴런에서 시그모이드 함수를 지나게 되는데 시그모이드 함수가 리턴하는 결과값은 은닉층 뉴런의 최종 출력값이다.
h_1과 h_2의 결과값은 아래와 같다.
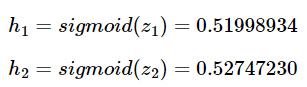
h_1과 h_2는 다시 출력층의 뉴런으로 향하게 되는데 이떄 다시 각각의 값에 해당되는 가중치와 곱해지고, 다시 가중합 되어 출력층 뉴런의 시그모이드 함수의 입력값이 된다.

z_3과 z_4이 출력층 뉴련에서 시그모이드 함수를 지난 값은 이 인공 신경망이 최종적으로 계산한 출력값이다.

오차를 계산하기 위한 손실 함수로는 평균 제곱 오차 MSE를 사용한다.
식에서는 실제값을 target이라고 표현하며, 순전파를 통해 나온 예측값을 output이라고 표현한다.
각 오차를 모두 더하면 전체 오차가 된다.
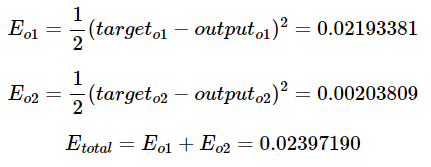
3. 역전파 단계(BackPropagation Step)
순전파가 입력층에서 출력층으로 향한다면 역전파는 반대로 출력층에서 입력층 방향으로 계산하면서 가중치를 업데이트 해간다.
출력층 바로 이전의 은닉층을 N층이라고 했을 때, 출력층과 N층 사이의 가중치를 업데이트 하는 단계를 역전파 1단계, N층과 N층의 이전층 사이의 가중치를 업데이트 하는 단계를 2단계라고 하자.

역전파 1단계에서 업데이트 해야할 가중치는 총 4개이다.
W_5부터 업데이트 해보자면 오차의 미분값을 계산해야 한다.
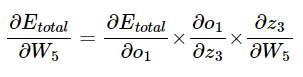

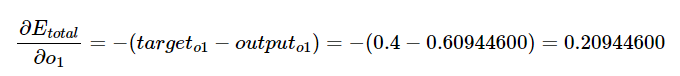
시그모이드 함수의 미분은 f(x)*(1-f(x))이다.
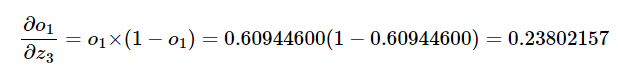


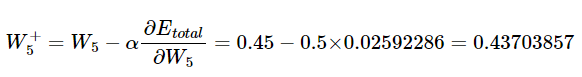
'Background > Pytorch 기초' 카테고리의 다른 글
| 과적합(Overfitting)을 막는 방법들 (0) | 2022.01.17 |
|---|---|
| 비선형 활성화 함수(Activation function) (0) | 2022.01.17 |
| 퍼셉트론(Perceptron) (0) | 2022.01.16 |
| 머신 러닝 용어 이해하기 (0) | 2022.01.16 |
| 소프트맥스 회귀로 MNIST 데이터 분류하기 (0) | 2022.01.16 |



