| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 융합연구
- panoptic segmentation
- NERF
- 경희대
- docker
- 딥러닝
- pytorch
- ICCV
- linux
- 논문
- ICCV 2021
- CVPR
- CVPR2023
- GAN
- Semantic Segmentation
- panoptic nerf
- NeRF paper
- 논문 리뷰
- 파이토치
- Deep Learning
- IROS
- paper review
- 논문리뷰
- 2022
- Computer Vision
- Neural Radiance Field
- Python
- Vae
- Paper
- 리눅스
- Today
- Total
윤제로의 제로베이스
Light Field Networks: Neural Scene Representations with Single-Evaluation Rendering 본문
Light Field Networks: Neural Scene Representations with Single-Evaluation Rendering
윤_제로 2022. 11. 23. 18:07NeRF: Neural Radiance Filed
기본적으로 NeRF는 View Synthesis Task를 수행하는 model이다.
View Synthesis란 여러 시점 이미지로부터 임의의 시점에서의 이미지를 예측하는 것을 의미한다.
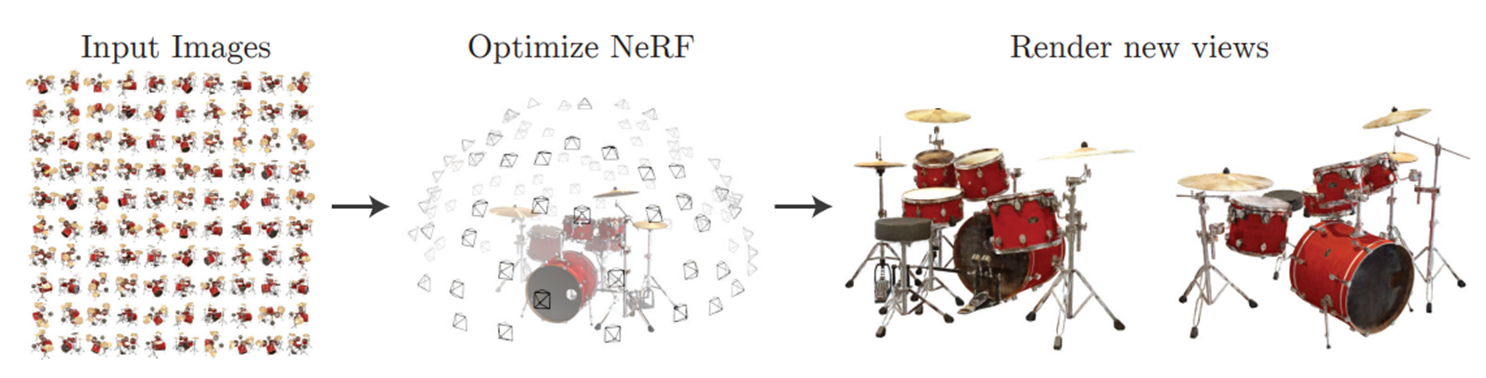
이를 수행하기 위해서 우리가 알아야하는 것은 바로 3D의 정보를 알아야 한다.
그래야 3D에 대해서 새로운 시점에서 바라본 2D 이미지를 예측할 수 있기 때문이다.
그렇다면 3D 정보는 어떻게 담을 수 있을까?
우리는 흔히 2D 정보를 pixel단위로 image에 담는다.

하나의 pixel 위치에 RGB 값을 담으면 그 것이 2D 정보를 담은 것과 같은 것이다.
하지만 이걸 3D에 적용하면 어떨까?
이를 3D 차원에선 흔히 'voxel'이라고 한다. 쉽게 생각해서 pixel의 3D화 라고 생각하면 된다.
voxel은 비교적 쉽게 떠올릴 수 있는 방법일 수 있으나 이 방법에 한계가 존재한다. 바로 너무 큰 용량을 요한다는 것이다.
voxel의 경우 빈 공간도 모두 저장해야하기 때문에 빈 공간이라는 불필요한 공간을 저장한다는 한계가 있다.
그래서 NeRF에서는 Implicit Representation을 사용한다.
'implicit'이라는 단어처럼 3D정보를 내포하는 Neural Network를 훈련시키는 것이다.
다시 말해 Neural Network를 하나의 function으로 하여금 3D정보를 갖고 있게끔 만드는 것이다.
즉 알고싶은 부분에 대한 3D 정보를 Network에 물어보면 이에 대한 정보를 Network가 알려주는 것이다.
NeRF는 3D location 정보로 (x,y,z)와 2D viewing direction(𝜃,𝜙)를 MLP 모델에 넣어주고 output으로 그 x,y,z 위치에서의 color RGB값과 volume density 𝜎값을 얻게 된다. 이때 나오는 RGB 값과 volume density를 weighted sum을 하여 pixel에 보일 rgb 값을 예측하는 것이다.

이때 하나의 pixel의 rgb를 얻기 위해서 한 Ray 위에 많은 point 들을 sampling하여 이 point들의 RGB와 density들의 합을 합치게 되는 것이다.
하지만 NeRF의 단점은 ray 당 수백번의 평가가 필요하게 된다는 점이다.
ray 하나당 sampling하는 point들의 개수가 192개이다. 그렇다면 이 192개들의 포인트들의 RGB와 volume density들을 얻은 후 weighted sum을 다 진행해야 하나의 pixel을 얻을 수 있다는 것이다.
Light Field Networks

NeRF의 단점인 수많은 연산과 학습하는데 오래걸린다는 점을 보완하여 Light Field Network가 나왔다.
Light Field의 차이점은 바로 'Ray를 input으로 넣으면 바로 RGB를 얻을 수 있다'는 것이다.
Light Field는 3가지 방식으로 NeRF의 단점을 이겨내려고 했다.
- Parameterization
- LFNs Geometry
- Meta-Learning
1. Parameterization
Parameterization에서는 input으로 들어가는 차원을 확 줄이면서도 unique하게 표현할 수 있도록 만들었다.
Plücker coordinates이라는 기법을 사용하여서 표현하는 것이다.
일단 Light Field Network를 사용하기 위해서는 카메라의 intrinsic parameter와 extrinsic parameter가 필요하다. 이를 알면 카메라의 현재 위치를 알 수 있다.
현재 위치를 알면 원점으로 부터 ray를 향하는 벡터를 알 수 있고, ray는 현재 카메라 위치와 pixel 좌표를 통해 알 수 있다. 이 두 벡터의 외적을 통해 ray와 원점이 동시에 존재하는 plane를 찾을 수 있고 이 plane에 수직하는 벡터를 찾을 수 있다는 것이다. 이를 ray를 표현하는 방식에 사용한다.

2. Geometry
시간면에서도 빠르게 연산이 가능한 Light Field Network이지만 단점은 depth를 구하기 어렵다는 것이다.
NeRF의 경우point sampling을 모두 하기 때문에 point의 depth를 비교적 쉽게 구할 수 있다.
하지만 LFNs의 경우 ray에서 보여질 rgb만을 구하기 때문에 depth를 쉽게 얻기엔 어려움이 있을 수 있다.
이때 사용하는 방식이 바로 Epipolar Plane 기법이다.

수식적인 면은 이해하기 어려움으로 직관적으로 표현하자면
1) 가장 먼저 plane을 하나 정한다. 평행한 2개의 벡터(위 그림에서는 a,b)를 정하여서 plane을 정한다.
2) 그 후 두 벡터위를 지나는 스칼라 점 t,s를 정하여 그 두 점을 정하는 ray를 만든다.
3) 이 Ray당 보이는 rgb값을 s,t에 관한 그림으로 표현한다.
이때 나오는 같은 색상의 직선을 통해서 직선의 기울기를 통해 이 point에 대한 depth를 수학적으로 계산할 수 있다!

'Self Paper-Seminar > NeRF' 카테고리의 다른 글
| Panoptic NeRF: 3D-to-2D Label Transfer for Panoptic Urban Scene Segmentation (0) | 2023.05.01 |
|---|---|
| Panoptic NeRF (0) | 2023.04.26 |
| Learning Object-Compositional Neural Radiance Field for Editable Scene Rendering(ICCV 2021) (0) | 2023.04.02 |
| GNeRF: GAN-based Neural Radiance Field without Posed Camera(ICCV 2021) (0) | 2023.04.02 |
| Point-NeRF: Point-based Neural(CVPR2022) (0) | 2023.01.12 |



